También te gustará:
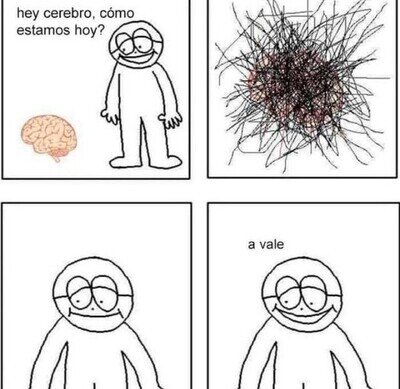
Mi cerebro un día tranquilo

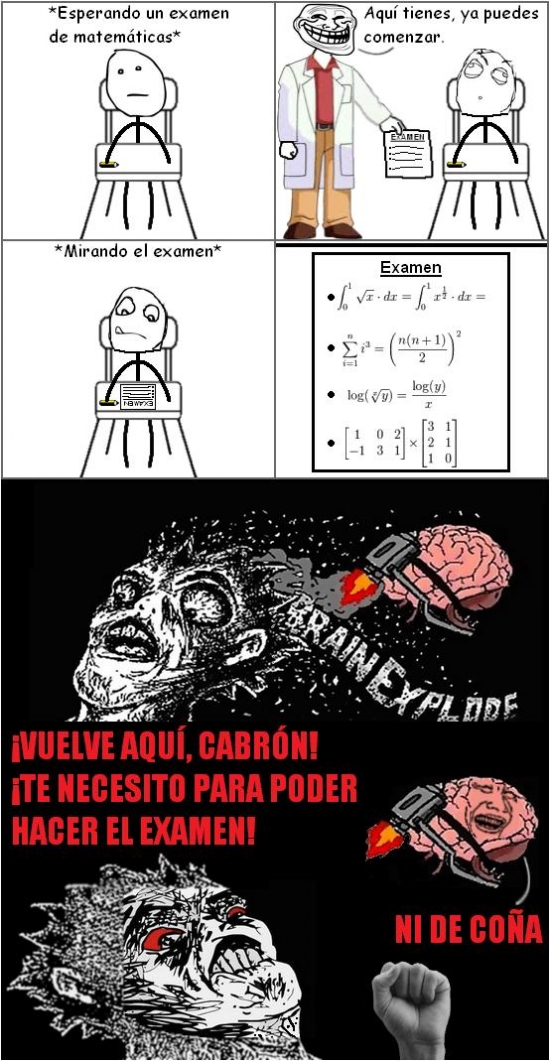
No me puede volver a pasar

No era momento para sus experimentos
Comentarios(60)
Por mejores
Por orden cronológico
Para ver este comentario debes Inciar Sesión o Registrarte.
55
Para ver este comentario debes Inciar Sesión o Registrarte.
52
Para ver este comentario debes Inciar Sesión o Registrarte.
51
Para ver este comentario debes Inciar Sesión o Registrarte.
15
Para ver este comentario debes Inciar Sesión o Registrarte.
13
Para ver este comentario debes Inciar Sesión o Registrarte.
12
Para ver este comentario debes Inciar Sesión o Registrarte.
11
Para ver este comentario debes Inciar Sesión o Registrarte.
7
Para ver este comentario debes Inciar Sesión o Registrarte.
6
Para ver este comentario debes Inciar Sesión o Registrarte.
4
Para ver este comentario debes Inciar Sesión o Registrarte.
3
Para ver este comentario debes Inciar Sesión o Registrarte.
3
Para ver este comentario debes Inciar Sesión o Registrarte.
3
Para ver este comentario debes Inciar Sesión o Registrarte.
3
Para ver este comentario debes Inciar Sesión o Registrarte.
2
Para ver este comentario debes Inciar Sesión o Registrarte.
2
Para ver este comentario debes Inciar Sesión o Registrarte.
2
Para ver este comentario debes Inciar Sesión o Registrarte.
2
Para ver este comentario debes Inciar Sesión o Registrarte.
2
Para ver este comentario debes Inciar Sesión o Registrarte.
2
Para ver este comentario debes Inciar Sesión o Registrarte.
2
Para ver este comentario debes Inciar Sesión o Registrarte.
2
Para ver este comentario debes Inciar Sesión o Registrarte.
1
Para ver este comentario debes Inciar Sesión o Registrarte.
1
Para ver este comentario debes Inciar Sesión o Registrarte.
1
Para ver este comentario debes Inciar Sesión o Registrarte.
1
Para ver este comentario debes Inciar Sesión o Registrarte.
1
Para ver este comentario debes Inciar Sesión o Registrarte.
1
Para ver este comentario debes Inciar Sesión o Registrarte.
1
Para ver este comentario debes Inciar Sesión o Registrarte.
1
Para ver este comentario debes Inciar Sesión o Registrarte.
1
Para ver este comentario debes Inciar Sesión o Registrarte.
1
Para ver este comentario debes Inciar Sesión o Registrarte.
1
Para ver este comentario debes Inciar Sesión o Registrarte.
1
Para ver este comentario debes Inciar Sesión o Registrarte.
1
Para ver este comentario debes Inciar Sesión o Registrarte.
1
Para ver este comentario debes Inciar Sesión o Registrarte.
1
Para ver este comentario debes Inciar Sesión o Registrarte.
0
Para ver este comentario debes Inciar Sesión o Registrarte.
0
Para ver este comentario debes Inciar Sesión o Registrarte.
0
Para ver este comentario debes Inciar Sesión o Registrarte.
0
Para ver este comentario debes Inciar Sesión o Registrarte.
0
Para ver este comentario debes Inciar Sesión o Registrarte.
0
Para ver este comentario debes Inciar Sesión o Registrarte.
0
Para ver este comentario debes Inciar Sesión o Registrarte.
0